Sposobnost izračunavanja volumena prostornih figura važna je pri rješavanju niza praktičnih problema iz geometrije. Jedna od najčešćih figura je piramida. U ovom članku ćemo razmotriti pune i skraćene piramide.

Piramida kao trodimenzionalna figura

Svi znaju za egipatske piramide, pa dobro znaju o kakvoj figuri ćemo govoriti. Međutim, egipatske kamene građevine samo su poseban slučaj ogromne klase piramida.

Geometrijski objekat koji se razmatra u opštem slučaju je poligonalna baza, čiji je svaki vrh povezan sa određenom tačkom u prostoru koja ne pripada ravni baze. Ova definicija vodi do figure koja se sastoji od jednog n-ugla i n trokuta.

Bilo koja piramida se sastoji od n+1 lica, 2*n ivica i n+1 vrhova. Budući da je figura o kojoj je riječ savršeni poliedar, brojevi označenih elemenata podliježu Ojlerovoj jednakosti:

2*n = (n+1) + (n+1) - 2.

Poligon koji se nalazi u bazi daje ime piramide, na primjer, trokutasta, peterokutna i tako dalje. Skup piramida sa različitim bazama prikazan je na fotografiji ispod.

Tačka u kojoj se spajaju n trouglova figure naziva se vrh piramide. Ako se okomica spusti s nje na bazu i ona je siječe u geometrijskom centru, tada će se takva figura zvati prava linija. Ako ovaj uslov nije ispunjen, tada se pojavljuje nagnuta piramida.

Prava figura čiju osnovu čini jednakostranični (jednakokutni) n-ugao naziva se pravilna.

Formula za zapreminu piramide

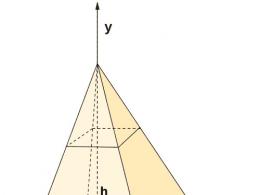
Za izračunavanje zapremine piramide koristićemo integralni račun. Da bismo to učinili, podijelimo figuru rezanjem ravnina paralelnih s bazom u beskonačan broj tankih slojeva. Na slici ispod prikazana je četvorougaona piramida visine h i dužine stranice L, u kojoj četvorougao označava tanak sloj preseka.

Površina svakog takvog sloja može se izračunati pomoću formule:

A(z) = A 0 *(h-z) 2 /h 2 .

Ovdje je A 0 površina baze, z je vrijednost vertikalne koordinate. Može se vidjeti da ako je z = 0, onda formula daje vrijednost A 0 .

Da biste dobili formulu za volumen piramide, trebali biste izračunati integral po cijeloj visini figure, odnosno:

V = ∫ h 0 (A(z)*dz).

Zamjenom zavisnosti A(z) i izračunavanjem antiderivata dolazimo do izraza:

V = -A 0 *(h-z) 3 /(3*h 2)| h 0 = 1/3*A 0 *h.

Dobili smo formulu za zapreminu piramide. Da biste pronašli vrijednost V, samo pomnožite visinu figure s površinom baze, a zatim rezultat podijelite sa tri.

Imajte na umu da je rezultirajući izraz valjan za izračunavanje volumena piramide bilo kojeg tipa. Odnosno, može biti nagnut, a njegova baza može biti proizvoljan n-ugao.

i njen volumen

Opšta formula za zapreminu dobijena u gornjem paragrafu može se precizirati u slučaju piramide sa pravilnom bazom. Površina takve baze izračunava se pomoću sljedeće formule:

A 0 = n/4*L 2 *ctg(pi/n).

Ovdje je L dužina stranice pravilnog poligona sa n vrhova. Simbol pi je broj pi.

Zamjenom izraza za A 0 u opću formulu, dobivamo volumen pravilne piramide:

V n = 1/3*n/4*L 2 *h*ctg(pi/n) = n/12*L 2 *h*ctg(pi/n).

Na primjer, za trokutastu piramidu, ova formula rezultira sljedećim izrazom:

V 3 = 3/12*L 2 *h*ctg(60 o) = √3/12*L 2 *h.

Za pravilnu četvorougaonu piramidu, formula zapremine ima oblik:

V 4 = 4/12*L 2 *h*ctg(45 o) = 1/3*L 2 *h.

Određivanje volumena pravilnih piramida zahtijeva poznavanje stranice njihove osnove i visine figure.

Krnja piramida

Pretpostavimo da smo uzeli proizvoljnu piramidu i odsjekli dio njene bočne površine koja sadrži vrh. Preostala figura naziva se skraćena piramida. Već se sastoji od dvije n-kutne baze i n trapeza koji ih povezuju. Ako je rezna ravnina bila paralelna s bazom figure, tada se formira skraćena piramida sa sličnim paralelnim osnovama. Odnosno, dužine strana jedne od njih mogu se dobiti množenjem dužine druge sa određenim koeficijentom k.

Na gornjoj slici prikazan je skraćeni pravilan, a vidi se da njegovu gornju osnovu, kao i donju, čini pravilan šestougao.

Formula koja se može izvesti korištenjem integralnog računa sličnog gore navedenom je:

V = 1/3*h*(A 0 + A 1 + √(A 0 *A 1)).

Gdje su A 0 i A 1 površine donje (velike) i gornje (male) baze, respektivno. Varijabla h označava visinu skraćene piramide.

Volumen Keopsove piramide

Zanimljivo je riješiti problem određivanja volumena koji najveća egipatska piramida sadrži u sebi.

Godine 1984. britanski egiptolozi Mark Lehner i Jon Goodman utvrdili su tačne dimenzije Keopsove piramide. Njegova prvobitna visina bila je 146,50 metara (trenutno oko 137 metara). Prosječna dužina svake od četiri strane konstrukcije iznosila je 230.363 metara. Osnova piramide je kvadratna sa velikom preciznošću.

Koristimo date brojke da odredimo zapreminu ovog kamenog diva. Budući da je piramida pravilna četverokutna, za nju vrijedi formula:

Zamjenom brojeva dobijamo:

V 4 = 1/3*(230,363) 2 *146,5 ≈ 2591444 m 3.

Zapremina Keopsove piramide je skoro 2,6 miliona m3. Za poređenje, napominjemo da olimpijski bazen ima zapreminu od 2,5 hiljada m 3. Odnosno, za popunjavanje cijele Keopsove piramide trebat će vam više od 1000 takvih bazena!

je poliedar koji je formiran od osnove piramide i presjeka koji je paralelan s njom. Možemo reći da je skraćena piramida piramida sa odsječenim vrhom. Ova figura ima mnoga jedinstvena svojstva:

• Bočne strane piramide su trapezi;
• Bočne ivice pravilne skraćene piramide su iste dužine i nagnute prema bazi pod istim uglom;
• Osnove su slični poligoni;
• U pravilnoj skraćenoj piramidi, lica su identični jednakokraki trapezi, čija je površina jednaka. Takođe su nagnuti prema bazi pod jednim uglom.

Formula za površinu bočne površine krnje piramide je zbir površina njenih stranica:

Budući da su stranice skraćene piramide trapezi, za izračunavanje parametara morat ćete koristiti formulu trapezoidno područje. Za pravilnu skraćenu piramidu možete primijeniti drugu formulu za izračunavanje površine. Pošto su sve njegove strane, lica i uglovi u osnovi jednaki, moguće je primeniti perimetre osnove i apoteme, a takođe i izvesti površinu kroz ugao u osnovi.

Ako se, prema uvjetima u pravilnoj skraćenoj piramidi, daju apotema (visina stranice) i dužine stranica baze, tada se površina može izračunati kroz poluproizvod zbira opsega osnove i apotema:

Pogledajmo primjer izračunavanja bočne površine skraćene piramide.
Zadata je pravilna petougaona piramida. Apothem l= 5 cm, dužina ivice u velikoj osnovi je a= 6 cm, a ivica je na manjoj bazi b= 4 cm Izračunajte površinu skraćene piramide.

Prvo, pronađimo perimetre baza. Pošto nam je data petougaona piramida, razumemo da su osnove petougao. To znači da baze sadrže figuru sa pet identičnih strana. Nađimo opseg veće baze:

Na isti način nalazimo perimetar manje baze:

Sada možemo izračunati površinu pravilne skraćene piramide. Zamijenite podatke u formulu:

Tako smo izračunali površinu pravilne skraćene piramide kroz perimetre i apotemu.

Drugi način za izračunavanje bočne površine pravilne piramide je formula kroz uglove u osnovi i površinu samih ovih osnova.

Pogledajmo primjer izračuna. Sjećamo se da se ova formula odnosi samo na pravilnu skraćenu piramidu.

Neka je data pravilna četvorougaona piramida. Ivica donje osnove je a = 6 cm, a ivica gornje osnove je b = 4 cm. Diedarski ugao u osnovi je β = 60°. Nađite površinu bočne površine pravilne skraćene piramide.

Prvo, izračunajmo površinu baza. Pošto je piramida pravilna, sve ivice baza su jedna drugoj. S obzirom na to da je osnova četverokut, razumijemo da će biti potrebno izračunati površina trga. To je umnožak širine i dužine, ali kada su na kvadrat ove vrijednosti su iste. Nađimo površinu veće baze:


Sada koristimo pronađene vrijednosti za izračunavanje bočne površine.

Poznavajući nekoliko jednostavnih formula, lako smo izračunali površinu bočnog trapeza skraćene piramide koristeći različite vrijednosti.

Piramida. Krnja piramida

Piramida je poliedar, čije je jedno lice mnogougao ( baza ), a sva ostala lica su trokuti sa zajedničkim vrhom ( bočne strane ) (Sl. 15). Piramida se zove ispravan , ako je njegova osnova pravilan mnogougao i vrh piramide je projektovan u centar osnove (Sl. 16). Zove se trouglasta piramida čiji su svi rubovi jednaki tetraedar .

Lateralno rebro piramide je strana bočne strane koja ne pripada osnovici Visina piramida je udaljenost od njenog vrha do ravni baze. Sve bočne ivice pravilne piramide su jednake jedna drugoj, sve bočne strane su jednaki jednakokraki trouglovi. Visina bočne strane pravilne piramide povučena iz vrha naziva se apothem . Dijagonalni presjek naziva se presjek piramide ravninom koja prolazi kroz dvije bočne ivice koje ne pripadaju istoj površini.

Bočna površina piramida je zbir površina svih bočnih strana. Ukupna površina naziva se zbir površina svih bočnih strana i baze.

Teoreme

1. Ako su u piramidi sve bočne ivice jednako nagnute prema ravni osnove, tada se vrh piramide projektuje u centar kružnice opisane u blizini baze.

2. Ako su sve bočne ivice piramide jednake dužine, tada se vrh piramide projektuje u centar kružnice opisane blizu osnove.

3. Ako su sva lica u piramidi podjednako nagnuta prema ravni osnove, tada se vrh piramide projektuje u centar kruga upisanog u bazu.

Za izračunavanje zapremine proizvoljne piramide, ispravna formula je:

Gdje V- zapremina;

S baza– bazna površina;

H– visina piramide.

Za pravilnu piramidu ispravne su sljedeće formule:

Gdje str– perimetar baze;

h a– apotema;

H- visina;

S puna

S strana

S baza– bazna površina;

V– zapremina pravilne piramide.

Krnja piramida naziva se dio piramide zatvoren između osnove i rezne ravni paralelne sa osnovom piramide (slika 17). Pravilna skraćena piramida naziva se dio pravilne piramide zatvoren između osnove i rezne ravni paralelne s osnovom piramide.

Grounds skraćena piramida - slični poligoni. Bočne strane – trapezi. Visina krnje piramide je rastojanje između njenih osnova. Dijagonala skraćena piramida je segment koji povezuje njene vrhove koji ne leže na istoj površini. Dijagonalni presjek je presjek skraćene piramide ravninom koja prolazi kroz dvije bočne ivice koje ne pripadaju istoj površini.

Za skraćenu piramidu važe sljedeće formule:

(4)

Gdje S 1 , S 2 – površine gornje i donje osnove;

S puna– ukupna površina;

S strana– bočna površina;

H- visina;

V– zapremina krnje piramide.

Za pravilnu skraćenu piramidu formula je tačna:

Gdje str 1 , str 2 – perimetri osnova;

h a– apotema pravilne krnje piramide.

Primjer 1. U pravilnoj trouglastoj piramidi, ugao diedara u osnovi je 60º. Pronađite tangentu ugla nagiba bočne ivice prema ravni baze.

Rješenje. Napravimo crtež (slika 18).

Piramida je pravilna, što znači da se u osnovi nalazi jednakostranični trougao, a sve bočne strane su jednaki jednakokraki trouglovi. Diedarski ugao u osnovi je ugao nagiba bočne strane piramide prema ravni osnove. Linearni ugao je ugao a između dvije okomice: itd. Vrh piramide projektovan je u centar trougla (središte opisane i upisane kružnice trokuta ABC). Ugao nagiba bočne ivice (npr S.B.) je ugao između samog ruba i njegove projekcije na ravan baze. Za rebro S.B. ovaj ugao će biti ugao SBD. Da biste pronašli tangentu, morate znati noge SO I O.B.. Neka je dužina segmenta BD jednako 3 A. Dot O linijski segment BD je podijeljen na dijelove: i Od nalazimo SO: Od nalazimo:

odgovor:

Primjer 2. Nađite zapreminu pravilne skraćene četvorougaone piramide ako su dijagonale njenih osnova jednake cm i cm, a visina 4 cm.

Rješenje. Da bismo pronašli zapreminu krnje piramide, koristimo formulu (4). Da biste pronašli površinu baza, morate pronaći stranice osnovnih kvadrata, znajući njihove dijagonale. Stranice osnovica su jednake 2 cm odnosno 8 cm.To znači površine osnova i Zamjenom svih podataka u formulu izračunavamo zapreminu krnje piramide:

odgovor: 112 cm 3.

Primjer 3. Nađite površinu bočne strane pravilne trokutaste skraćene piramide čije su stranice osnova 10 cm i 4 cm, a visina piramide 2 cm.

Rješenje. Napravimo crtež (slika 19).

Bočna strana ove piramide je jednakokraki trapez. Da biste izračunali površinu trapeza, morate znati osnovu i visinu. Osnove su date prema uslovu, samo visina ostaje nepoznata. Naći ćemo je odakle A 1 E okomito iz tačke A 1 na ravni donje baze, A 1 D– okomito od A 1 per AC. A 1 E= 2 cm, jer je ovo visina piramide. Naći DE Napravimo dodatni crtež koji prikazuje pogled odozgo (slika 20). Dot O– projekcija centara gornje i donje baze. budući da (vidi sliku 20) i S druge strane uredu– radijus upisan u krug i OM– radijus upisan u krug:

MK = DE.

Prema Pitagorinoj teoremi iz

Bočna površina lica:

odgovor:

Primjer 4. U osnovi piramide leži jednakokraki trapez, čije su osnove A I b (a> b). Svaka bočna strana formira ugao jednak ravni osnove piramide j. Pronađite ukupnu površinu piramide.

Rješenje. Napravimo crtež (slika 21). Ukupna površina piramide SABCD jednak zbroju površina i površine trapeza A B C D.

Upotrijebimo tvrdnju da ako su sva lica piramide podjednako nagnuta prema ravni baze, tada se vrh projektuje u središte kruga upisanog u bazu. Dot O– projekcija temena S u osnovi piramide. Trougao SOD je ortogonalna projekcija trougla CSD do ravni baze. Koristeći teoremu o površini ortogonalne projekcije ravne figure, dobijamo:

Isto tako znači Dakle, problem se sveo na pronalaženje površine trapeza A B C D. Nacrtajmo trapez A B C D odvojeno (sl. 22). Dot O– središte kruga upisanog u trapez.

Kako se kružnica može upisati u trapez, onda ili Iz Pitagorine teoreme imamo